Batch 3 - Class 248 - Computational Thinking 1
(zoom)
Pre-Class Exercise
- (CombProbs Problem 52) Can you arrange numbers 1..9 in a circle so that sum of two neighbors is never divisible by 3, 5 or 7
- Answer: 5,6,2,9,4,7,1,3,8,(5) - One way to do this is to figure out all combinations which are "allowed", i.e. not divisible by 3,5,7. Then start to work with constraints like number 2 can only go with 6 and 9, and build from there. Number 4 can only go with 9 and 7, so that extends the sequence to 6,2,9,4,7, and so on.
Attendance Kabir, Arjun, Mihir, Advay, Vansh, Raghav, Angad, Aarkin, Vivaan, Sidharth, Ayush, Aneesh, Harshiet, Rehaan, Shikhar
Class Notes:
Knight's Tour Problem
In a Knight's tour problem, a single chess knight is able to move on a board. A knight can move two steps in one direction and then one square in a perpendicular direction. It can jump over squares. Consider the following square, and try to figure out a Knight's tour where the knight starts from 1, and visits each square exactly once and returns back to 1.
Time yourself. However, do not just solve. Describe an algorithm, i.e. a method, to solve it. It could just be the list of numbers through which you must go. It could be instructions on how to go about it. The algorithm should be precise enough that another person can check your solution/algorithm without any ambiguity.
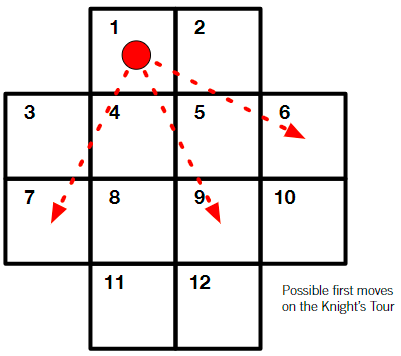
Pair up students to check each others' solutions/algorithms. Tabulate the time that each student took.
Hotel Tour Guide
You are a hotel guide and you must pick your guests at the hotel and take them to all the tourist attractions shown below. The guests would not like to go to the same place twice. Find the best way to do so, and bring them back to the hotel in the evening
Time yourselves. And write the algorithm. Remember, avoid ambiguity.
.png)
Tabulate the time taken - were you able to solve it faster than the Knights' tour problem, or slower.
What are the commonalities that you found in the two problems? (Let students talk about it)
Abstraction: There is a graph, with nodes and edges. Abstraction involves focusing on what is important and ignoring the rest - for example, we have not shown how much each tourist attraction cost for entry.
Generalization: Both problems are similar problems - ask students in what respect. Both problems involved going from one point to all other points and coming back to the original problem.
Algorithm: The method to solve the problem. How did you go about traversing the graph? For this kind of the problem, depth first is an intuitive route - you go down a path as far as you can and you backtrack if its the wrong path and try another one.
Pattern Matching: It seems that we can solve any "route finding" problem by drawing a graph for that - this is pattern matching.
However, in spirit of abstraction, does it matter how the chessboard looks? Does it have square of circular squares? May be we should just draw a graph corresponding to the chess board. Ask students how they would think about it - a node for each position, and an edge connecting two nodes where a knight can directly go from one node to other.
.png)
Can you try to simplify the graph? Untangle it.
Students should realize that as they untangle it, this graph is exactly the same as the tour guide problem. These two problems were not just the same kind of problem, they were the same problem.
.png)
Suppose you had a different board (or a different tube map and tourist attractions) - how would you think about a generalized way of solving it? What is a generalized algorithm?
- Let kids propose ideas, and see if starts to gravitate towards a depth first (or an alternate) approach.
Emphasize generalization, abstraction, pattern matching and algorithms to reinforce the elements of computational thinking.
Back to Homework Problem
Think about the homework problem listed above. It has some common elements - generalizations - with the other problems above.
- It has a set of places (the numbers 1..9),
- defined connectivity - any two numbers whose sum is not divisible by 3,5 or 7 can be "connected", i.e they can be next to one another, and
- a problem statement to line them up in a circle, which is same as saying that you have to visit them exactly once and come back to the original number.
Can you express the problem as a graph, and apply depth first search to solve?
What are you generalizing?
What are you abstracting?
How are you solving, i.e. the algorithm?
Do you see the pattern of problems with similar solution?
Homework:
- You have a telephone directory and you want to search for a particular name in there (for example, "Alok Mittal") - how would you do that?
- If you had to search for "Zach Burns", how would you do that?
- Does your method work if the name is not in the directory?
- Can you think about a common method regardless of what name you are searching?
- Is your method efficient? If not, how do you make it more efficient?
References: